Tutorial: Relativity, Cosmic Rays, and Accelerators
Some special relativity
If you have measure muon time of flight, you can calculate the speed of the muon and the Lorentz factor for the muons.
For example, if the distance the muons travel is, say, d = 10 m and the TOF is measured as t = 34.0 nanoseconds, then
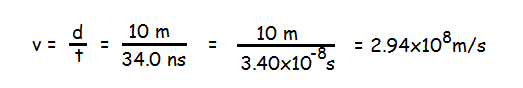
The fraction of the speed of light "beta" is
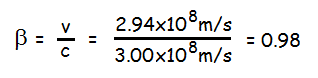
The Lorentz factor "gamma" is
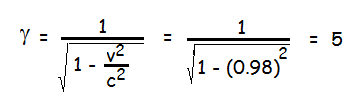
Another way to get "gamma" for a particle is to use the energy and mass relationship.
In our example, we can use E = γmc2 to find the energy of our muon, since we know the invariant mass of a muon is m = 106 MeV/c2:
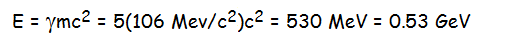
Application to accelerators
The ILC will be 30-50 km long and energize electrons and positrons to 250 GeV or more so that they will collide with energies upwards of 500 GeV:
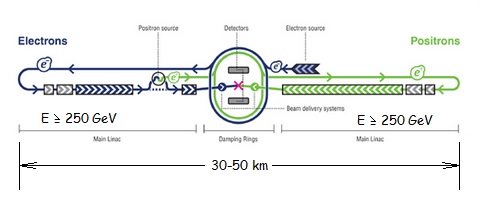
(Learn more in this Wikipedia article.)
Imagine we want to build a muon-antimuon collider about the size and energy of the ILC. We might want to do this to make a smaller collider with similar properties, because:
- Muon-antimuon and electron-positron collisions yield substantially the same results. Both are leptons with no structure we can detect, meaning the entire energy of the collion can go into creating one particle or particle pair, leaving no background.
- Muons are much more massive. The ratio of masses is mμ/me = (106 MeV/c2)/(0.511 MeV/c2) = 207. This means, in accelerating, they yield much less energy per unit mass and, therefore, it is more practical to build a circular collider (like the LHC) with counter-rotating beams. This saves space and makes it easier to build.
- In the LHC, the circulating beam allows physicists to collide the same bunches of beam particles again and again, so they do not have to be continually made and accelerated. A "fill" of beam particles in the accelerator can last up to 24 hours.
So, why not build a muon collider? Some people are working on this concept, most notably in the MICE experiment.
However, there is one other fact that is important to this: the lifetime of the muon is approximately 2.18 μs.
Let's think about this again after doing some calculations:
- In its own reference frame, how far does a 2 GeV muon travel in one lifetime? How far might it go in our reference frame, as observers? Does a cosmic ray muon travel far enough to reach the surface of earth if it is created at an altitude of 15 km? Explain.
- Now imagine that you have a 250 GeV muon (similar in energy to an electron in ILC). What is the value of gamma? Beta? What is its lifetime in our reference frame?
- How long will it take before a sample of 250 GeV muons has decayed so that only 1% are left in our reference frame? About how long would a "fill" be?
Discuss the benefits of a muon collider vs. the benefits of ILC.