|
Tiny URL for this page: http://tinyurl.com/s2n-rwr. Here one way for a teacher to get Rolling with Rutherford rolling with his or her students.
The goal and why: Students seek to find the diameter of a marble by indirect measurement. If a physicist wants to find the diameter of an atom in a crystal, for example, there is no question of using a ruler or a caliper. The atom is too small. Then she, like Rutherford, might fire particles at an array of those atoms and use numbers of hits and misses to figure out the size of the atom.
What you need:
|
|
Set-up: For each student group, print 3 copies of the template. Cut out the crossed holes on one of these. Align and tape the pages together; fold the edges to make a barrier on each side. Back the holes with tape so the sticky side faces out through the holes. Tape the whole assembly down on a flat surface. Place a marble on each hole. The result should look something like the image to the right. The places where the papers join should be completely taped over so that the path of a marble rolled from the beginning (where the single marble is in the image) to the end (past the 5 marbles) has as little obstruction to its course as possible, You should also make a 0-10 horizontal axis on the wall, in a window, or on a chalk/whiteboard. Label the axis as the number of hits out of 10. This will serve for the histogram you will make. |
 |
|
What happens: Each student gets 10 rolls of the marble. He or she must take care to roll toward the 5 target marbles but must not aim. Misses are as valid as hits. When a taget marble is hit, it should be noted and the target marble returned to its place. The sticky-side-up tape should help. The student will get a score: the number of hits out of 10. The student should then take a sticky note and put it above her or his score on the histogram. Even if you have multiple groups working, all students put their scores on the same histogram. Get others to try, e.g. an administrator who happens to be passing by. You want statistics. If you do this activity in multiple classes during the day, let the histogram build over the course of the day. Here is an example of building a histogram with a relatively small group in a workshop setting:
Note that, in the last frame, the group found a peak value of the number of hits out of 10. You should do the same with your students. Note also that the simplest version of calculation of the diameter of the target is used in the last frame. This does not take into account the size of the rolled marble: in workshop from which the images come, the group used targets much larger than the marble which was rolled. Thus, perhaps the simple approximation was acceptable. In our case, the target and the projectile are the same size. To analyze the data, you need:
The probability of a hit from the point of view of the experimental data is P = n/10. The probability of a hit for marbles of diameter D in the simple approximation above is P = ND/L, based on the fraction of distance L that is blocked by target marbles. Life is not that simple, of course, so we modify that equation based on what we know about the marbles and their collisions. |
|
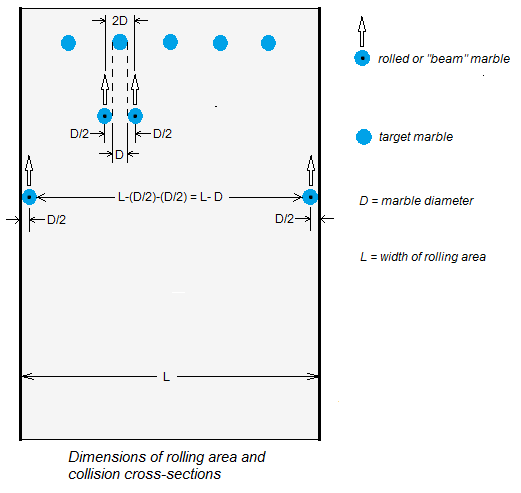
Looking at the diagram to the right, note that the center of the rolled marble can approach a target marble within a cross-section of 2D to make a collision. There are N target marbles, so the total target cross-section is N(2D). For the cross-section of the rolling area, the center of the rolled marble can get no less than D/2 from a side barrier; our actual rolling cross section is L-D. Thus we modify our original simple equation: P = [N(2D)] / (L-D). Set the probabilities from experiment and from calculation equal to each other, so (n/10) = (2ND) / (L-D). After some algebra, D = Ln / (20N+n). |
 |
|
Question: Do we "check" our result against a measurement made with a ruler? The physicist measuring those atoms has no such luxury. The indirect measurement is the measurement. Maybe we do, maybe we don't.
Resources:
|



