Relativity Concepts Tutorial

Submitted by kcecire
Published: | Group(s):
LHC Fellows Workspace

Divide into four groups. Each group is assigned to find answers for the Foundation Question plus one of the four Group questions. Each group presents to the other groups what they have learned.

 

Foundation Question for all 3 groups: How do we justify the Lorentz Time Dilation and Length Contraction equations of Special Relativity?

Rules:

  1. We use only inertial reference frames, that is, constant speeds only.
  2. The speed of light in a vacuum in invariant, that is, the same in all reference frames.

A consequence of the invariance of the speed of light is that time intervals seen by an observer in one reference from are different when observed from a differen reference frame. Consider a cart rolling at horizonal speed v. A flashlight fires a photon vertically upward. It goes some distance y in time t at the speed of light, so y = ct. In the reference frame of the cart, that is all the motion there is. It is only to a "stationary" observer that the cart also moves horizontal distance x. The observer records time to for this to happen, so x = vto. That same observer sees the photon go not just distance y but a diagonal distance s. Since it is a photon (light) and the speed of light us invariant, s = cto.

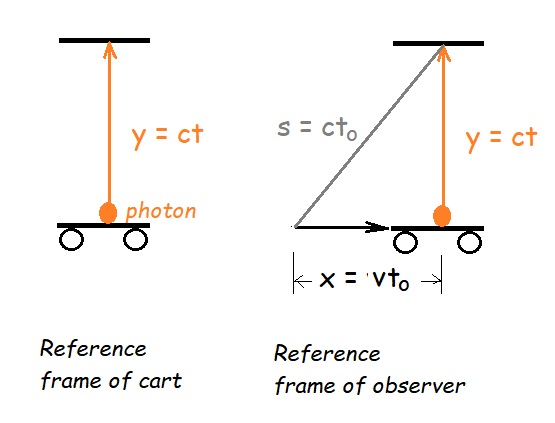
A. Using the Pythgorean Theorem, s2 = x2 + y2. Substitute ct, cto, and vto to find the relationship between the time t for the photon to travel in the reference frame of the moving cart and the time for the photon to travel its path in the frame of the observer.

B. Using similar triangles and substitutions, find the relationship between s and y. 

References:

 

Group 1 Question: What is the Michelson-Morley Experiment and why is it significant?

Group 2 Question: What is Galilean Relativity and how is it different from Einstein's Special Relativity?

Group 3 Question: What is General Relativity and how is it different from Special Relativity?

 

References: