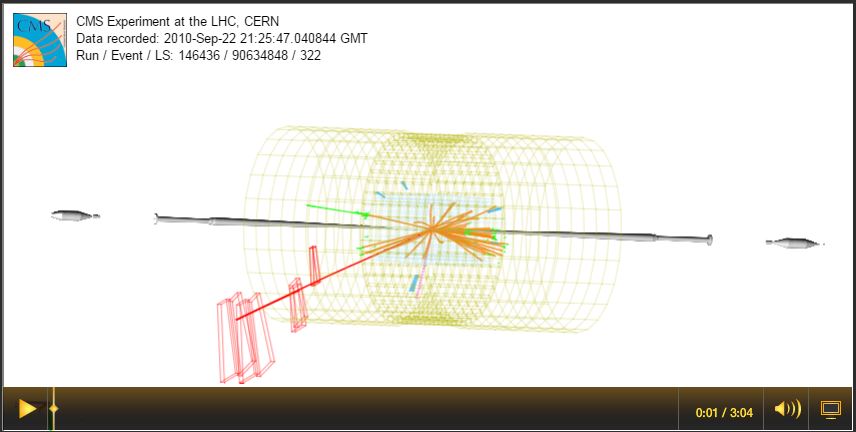
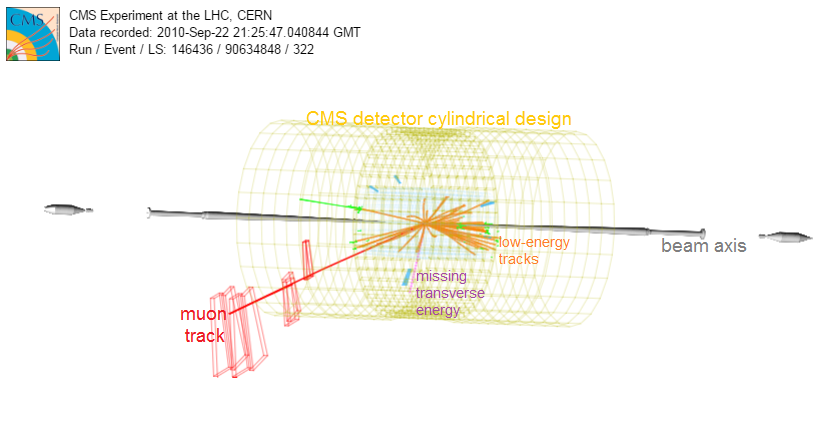
The detector for a collider should be able to wrap around and enclose the collision point as much as possible. So, here is what we need to know:
- The shape of the detector is roughly cylindrical
- The beam goes through the cylinder axis with collisions at the center of the detector.
- The beam axis is usually designated as the z-axis.
- The y-axis is perpendicular to the z-axis and vertical; +y is "up" toward the zenith.
- The x-axis is perpendicualr to the z-axis and horizontal; in the LHC, +x is toward the center of the accelerator ring.
- Physicists use polar angles φ and θ as well as an angle-like parameter η to describe the direction of a track or of the momentum vector of a particle.
To learn more, please choose the images below to open each of three instructional screencasts.
Overview of Screencast 1:
The CMS detector, shown in the computer-generated event display, has a roughly cylindrincal geometry with the beamline running through the axis of the cylinder. Protons rum down the beamline from either end and collide in the center. The beamline is designated as the z-axis. The x- and y-axes are perpendicular. We will explore how the direction of the muon in this event (long red track) can be shown as angles in reference to these axes.
|
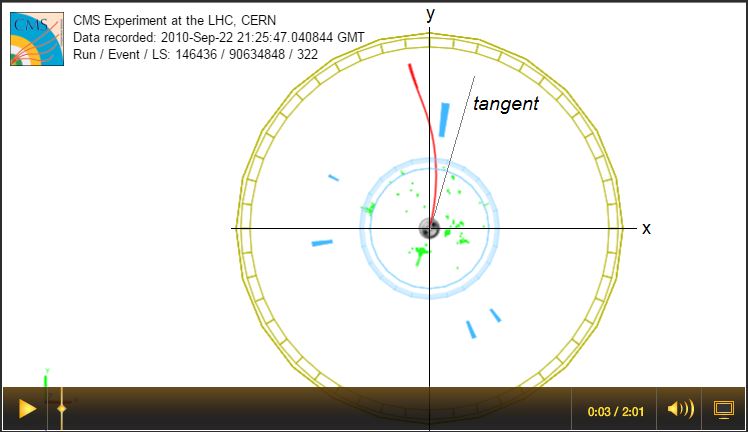
Overview of Screencast 2: In the x-y view, the beamline runs in and out of the page throught he center of the detector. In this view, the cylindrical shape appears as a circle. The x- and y-axes interesect the beamline at the center of the detector. The x-axis is horizontal and the y-axis is vertical in this view. The muon track curves in the magnetic field so we use the tangent line to refer to the initial direction of its momentum. Angle φ runs from the +x axis to the tangent line. The range of φ is 0 to 2π radians or 0o to 360o. |
Overview of Screencast 3:
In the r-z view, the beamline (z-axis) is horizontal and the radial distance r of the track (that is, the hypotenuse of the triangle formed by the x and y dimensions of the track) forms the vertical axis. Radial distance r is in the same direction as pt - see below. The angle from the +z axis to the muon track is labeled θ, which runs from 0 to π radians or 0o to 180o. However, θ is not as often used as a parameter called the pseudorapidity, η. The low energy tracks are shown here to help us understand one reason for this. Note that there are many more tracks close to the z-axis and few close to the x- and y-axes. The pseudorapidity is a parameter which runs from 0 a long radial distance r to positive or negative infinity as the track measures closer to the +z or -z axis and is set up to roughly equalize the number of tracks in equal intervals of η. It is also very nearly invariant, meaning its val;ue will staypretty much the same in the lab frame of reference or in tbe frame of reference of the particle itself.
Even more: note the components of the momentum vector of the muon.
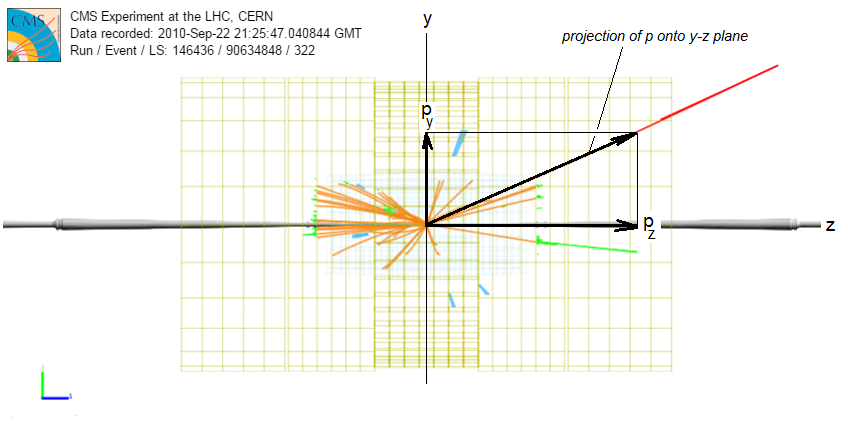
In this side (y-z) view, we see the momentum vector as projected onto the y-z plane. The z-component of the momentum is marked pz and goes along the beammline. This is also sometimes called the "forward momentum" (whether it goes in the +z or the -z direction) as opposed to the transverse momentum, described below. With the forward and transverse momenta and directions φ and η, the momentum vector of the particle is described completely.
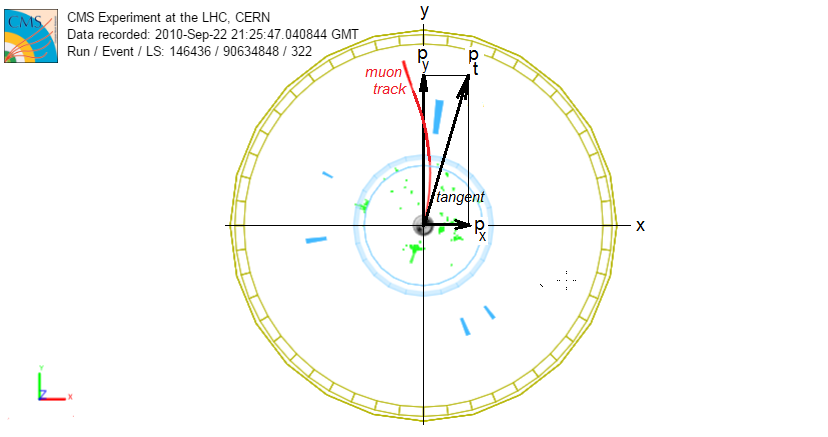
In the forward (x-y) view, we see the muon track is curved due to the solenoidal magnetic field of CMS. The momentum of the muon at the vertex, then, is tangential to the track. This vector is the transverse momentum pt of the muon because it makes a right angle with the beamline and is in the transverse (or x-y) plane. Its relationship to the x-and y-components of the momentum is pt2 = px2 + py2 and the net momentum of the particle is given by p2 = pt2 + pz2.