Understanding MINERvA Masterclass Results

Navigation

• MINERvA Masterclass Documentation 
• MINERvA Masterclass Guide
• Neutrino Masterclass Project Map
• MINERvA Masterclass website

This document is intended for masterclass leaders and physics teachers as a guide to explaining the results of the MINERvA masterclass to students. 

Pedagogy

Enduring Understanding:

Indirect evidence provides data to study phenomena that cannot be directly observed.

Objectives:

1. Apply conservation of momentum and energy to measure the approximate energy of a neutrino beam from the Fermilab accelerator complex.
2. Apply conservation of momentum and energy to measure the properties of neutrons in nuclei of atoms in the target of a neutrino beam.
3. Determine which events are signal events from which effective measurements may be made and which events are background that cannot be used for measurements.

Physics

Interaction:

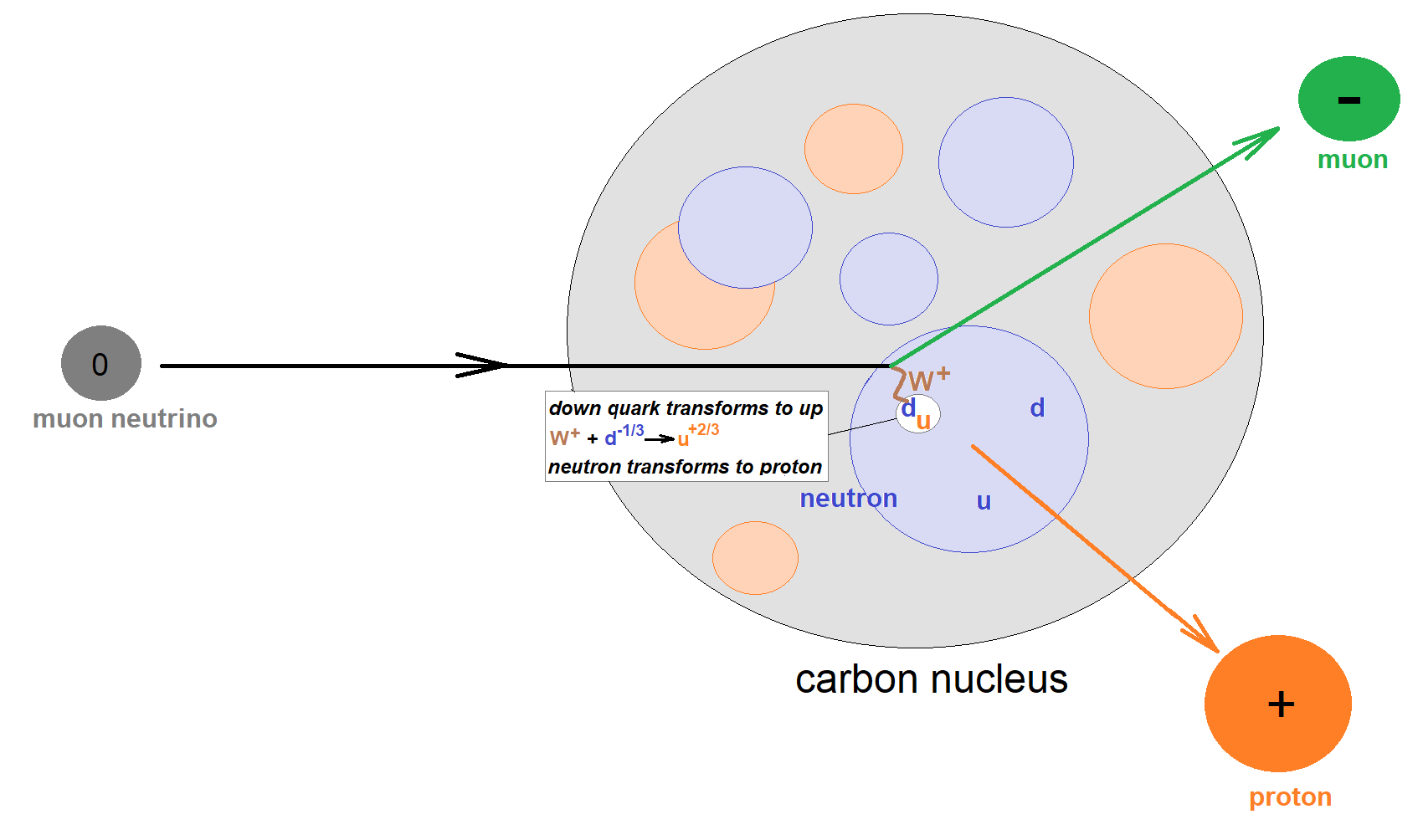
A muon neutrino encounters a carbon nucleus in the targer area of MINERvA. It strikes a neutron in the nucleus and interacts by emittiing a W+ boson. The W+ is absorbed by a down quark in the neutron, changing it to an up quark and transforming the neutron into proton. When the neutrino emits the W+, it transforms into a muon. Both the muon and the proton carry the original momentum of the neutrino and thus move rapidly away from the carbon nucleus into the detector modules.

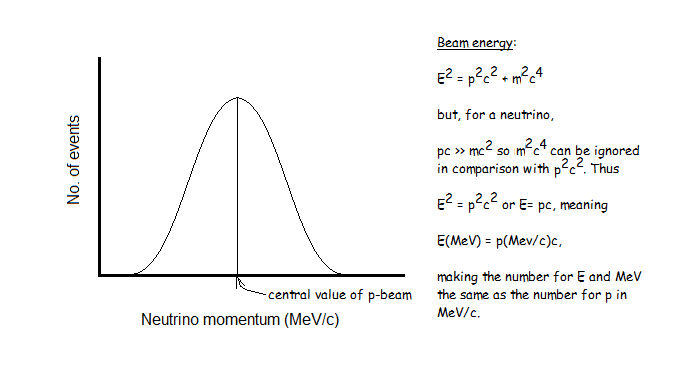
Beam momentum and energy:

The defined z-axis of the detector system is aligned to the direction of the Fermilab neutrino beam. The histogram of values of p_z should make a normal distribution with the peak at the central value of the neutrino momentum in MeV/c. Since the masses of the neutrinos are extremely small and the momenta are quite high, the same number in MeV is the beam energy.

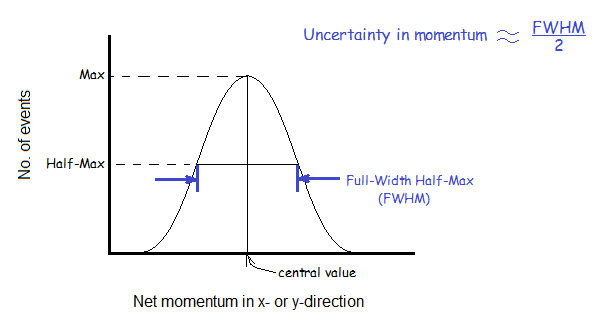
Momentum in x- and y-directions:

Since the momenta of the neutrinos are in the z-direction by definition, the net momenta they give to the outgoing protons and muons in the x- and y-directions must be zero. If the neutrons are initally rest before the interaction, then the histograms of net p_x and net p_y must peak at zero and be quite narrow. If there is a wide distribution, then the momenta in x and y must be random and mostly non-zero, producing a fairly wide normal distribution centerd on zero.

The uncertainty in the distribution of p_x or p_y can be estimated as half of the Full Width Half Maximum (FWHM/2). To find this, find the level halfway below the peak and measure the width of the distribution at that point. Divide by 2.

Radius of Carbon Nucleus:

The radius of an atomic nucleus in Fermi (fm; 1 fm = 10^-15m) is extimated using the equation 

R = (1.25 fm)A^1/3,

where A is the atomic mass number. For carbon, A = 12 and therefore

R = (1.25 fm)(12^1/3) = 2.7 fm.

If the neutrons in carbon have their own momenta then they are constrained in their movement by the radius of the nucleus. If we understand the process of the neutron-neutrino interaction and resulting ejection of the proton and muon well enough, our x- and y-momentum data analysis should yield a reasonable estimate of this distance-of-travel constraint, that is, 2.7 fm, as the uncertainty in position of the neutron.

Calculation of Δx or Δy:

We shall examine Δx only as the analysis of Δy is identical. 

The Heisenburg Uncertainty Principle states that the uncertainties in position and momentum form a complimentary pair, the products of which are no smaller than Planck's constant divided by 4π, or

Δp_xΔx ≥ h/4π.

Using momentum in MeV/c and distance in fm, it turns out that h/4π is about 150 MeV-fm/c. However, this assumes that the neutron is completely free to move. It is not as it is bound to quantized energy states in the nucleus and no two of them can occupy the same state due to the Pauli Exclusion Principle. A collection of particles that behaves this way is called a Fermi Gas; the Fermi Gas approximation of the behavior of the neutrons just about doubles the constant in the Uncertainty Principle to 300 MeV-fm/c. Then the uncertainty in x is estimated as

Δx = (300 MeV-fm/c) / Δp_x.

If this number is significantly less that the carbon nuclear radius of about 2.7 fm, then there is more physics needed to fully understand the interaction. Getting the interaction right is one of the main purposes of MINERvA and is needed to make precision measurments of neutrinos in DUNE.

Addendum:

Rick Dower of the Boston QuarkNet Center prepared a thorough treatment showing mathematically how the distributions in momentum must be from quantum effects and not from thermal noise: Neutrino Target Motion.