CMS e-Lab Library
Submitted by kcecire
on Friday, September 16, 2016 - 10:58
Resources

CMS e-Lab, production, https://www.i2u2.org/elab/cms
CMS e-Lab, development, http://i2u2-dev.crc.nd.edu/elab/cms
Screencasts for use of new CMS e-Lab data interface:
- J/Psi mass plot, http://screencast.com/t/m9QDaF4p
- 100k diumuon mass plot, https://www.screencast.com/t/OyrNQ2iqs
- Tour of the e-Lab, https://www.screencast.com/t/gLVOiKezG (ver 1) and https://www.screencast.com/t/K8zvHZ8lk3 (ver 2)
Additional Screencasts:
- DELPHI events, http://www.screencast.com/t/NTA2ODBiZTI
- Making a dimuon histogram, https://www.screencast.com/t/wEr4TTTdY
- iSpy-webgl event display, https://www.screencast.com/t/SLQyyXy8
Resources from this Library:
Geometry of a Collider Detector
Geometry of a Collider Detector

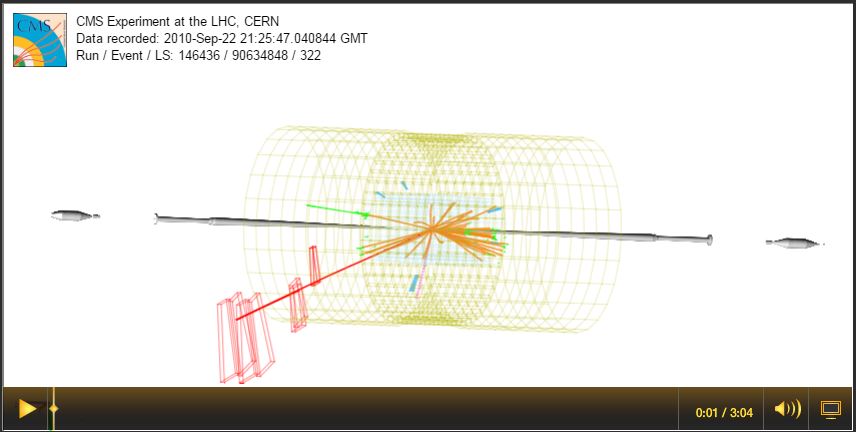
https://screencast-o-matic.com/watch/cY6rFL7LcqThe detector for a collider should be able to wrap around and enclose the collision point as much as possible. So, here is what we need to know:
- The shape of the detector is roughly cylindrical
- The beam goes through the cylinder axis with collisions at the center of the detector.
- The beam axis is usually designated as the z-axis.
- The y-axis is perpendicular to the z-axis and vertical; +y is "up" toward the zenith.
- The x-axis is perpendicualr to the z-axis and horizontal; in the LHC, +x is toward the center of the accelerator ring.
- Physicists use polar angles φ and θ as well as an angle-like parameter η to describe the direction of a track or of the momentum vector of a particle.
To learn more, please choose the images below to open each of three instructional screencasts.
|
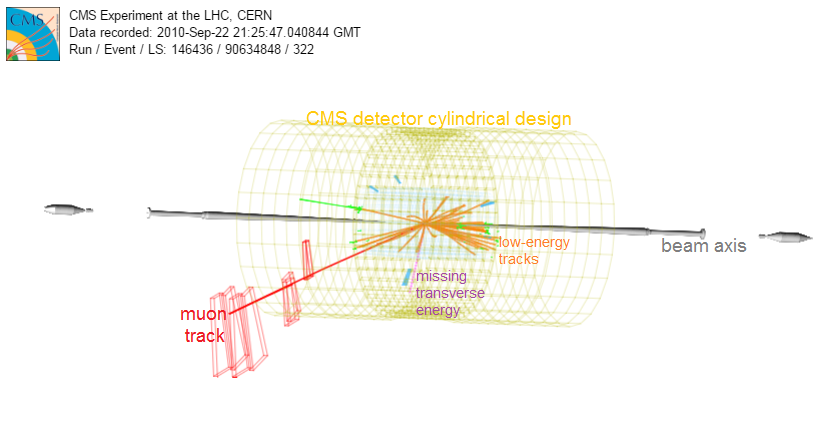
Overview of Screencast 1: The CMS detector, shown in the computer-generated event display, has a roughly cylindrincal geometry with the beamline running through the axis of the cylinder. Protons rum down the beamline from either end and collide in the center. The beamline is designated as the z-axis. The x- and y-axes are perpendicular. We will explore how the direction of the muon in this event (long red track) can be shown as angles in reference to these axes. |
|
|
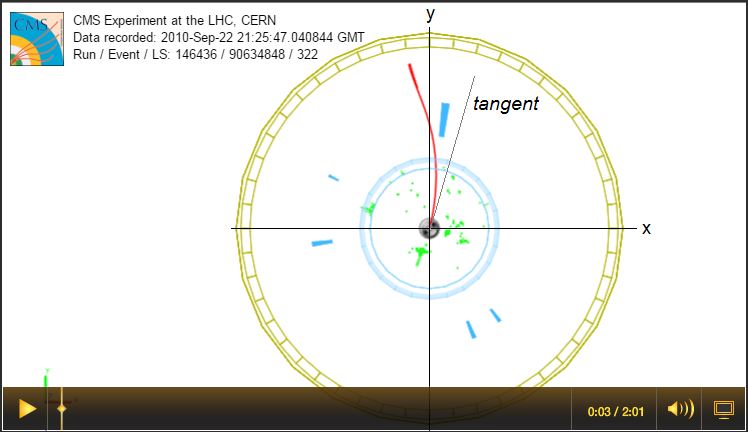
Overview of Screencast 2: In the x-y view, the beamline runs in and out of the page throught he center of the detector. In this view, the cylindrical shape appears as a circle. The x- and y-axes interesect the beamline at the center of the detector. The x-axis is horizontal and the y-axis is vertical in this view. The muon track curves in the magnetic field so we use the tangent line to refer to the initial direction of its momentum. Angle φ runs from the +x axis to the tangent line. The range of φ is 0 to 2π radians or 0o to 360o. |
|
|
Screencast 3: The y-z view with angle θ and pseudorapidity η. |
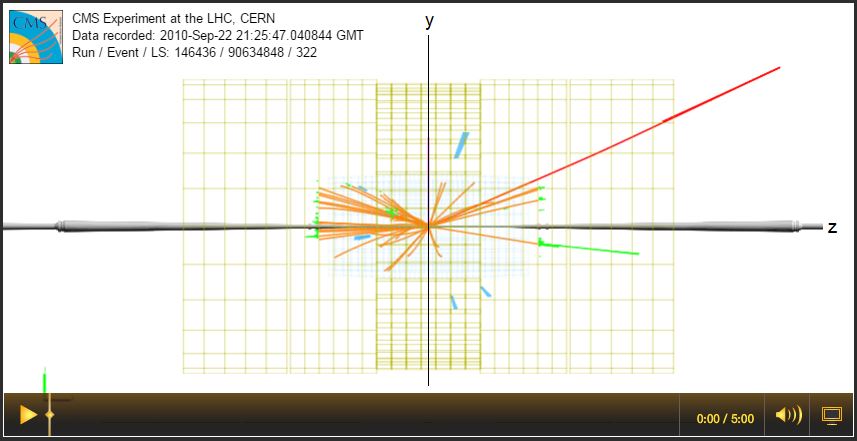
Overview of Screencast 3: In the y-z view, the beamline (z-axis) is horizontal and the y-axis is vertical. The x-axis is in and out of the image perpendicular to the other two axes. The angle from the +z axis to the muon track is labeled θ, which runs from 0 to π radians or 0o to 180o. However, θ is not as often used as a parameter called the pseudorapidity, η. The low energy tracks are shown here to help us understand one reason for this. Note that there are many more tracks close to the z-axis and few close to the x- and y-axes. The pseudorapidity is a parameter which runs from 0 at the +y -axis to positive or negative infinity +z or -z axis and is set up to roughly equalize the number of tracks in equal intervals of η. |
Even more: note the componenents of the momentum vector of the muon.
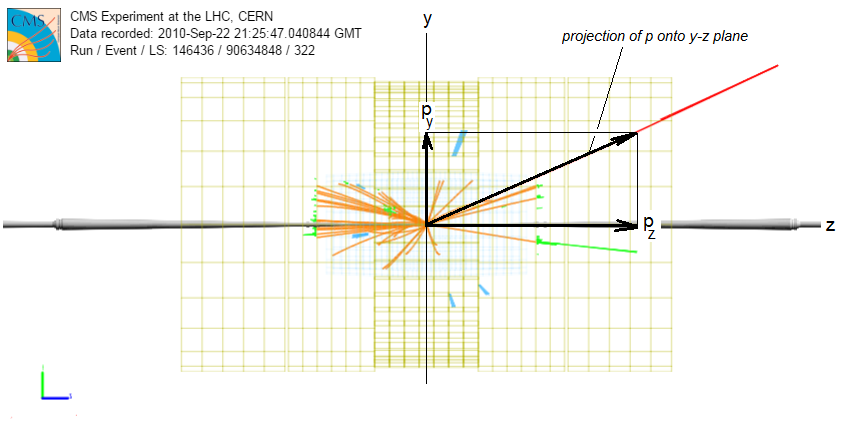 |
Comments: In the side (y-z) view, we see the momentum vector as projected onto the y-z plane. The z-component of the momentum is marked pz and goes along the beammline. This is also sometimes called the "forward momentum" (whether it goes in the +z or the -z direction) as opposed to the transverse momentum, described below. With the forward and transverse momenta and directions φ and η, the momentum vector of the particle is described completely. |
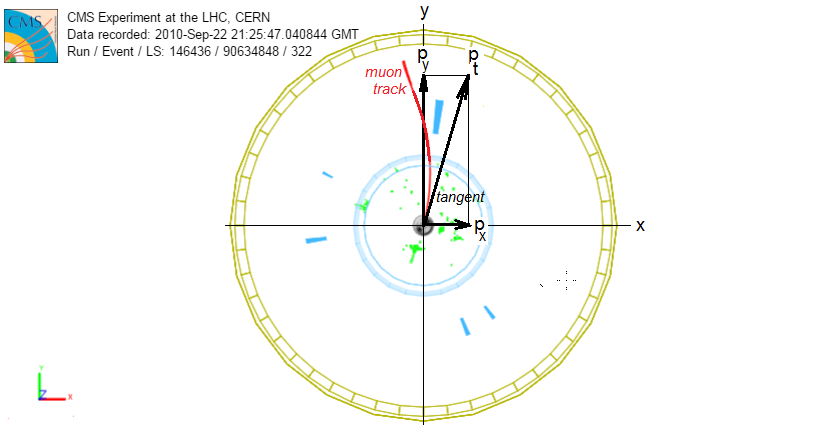 |
Comments: In the forward (x-y) view, we see the muon track is curved due to the solenoidal magnetic field of CMS. The momentum of the muon at the vertex, then, is tangential to the track. This vector is the transverse momentum pt of the muon because it makes a right angle with the beamline and is in the transverse (or x-y) plane. Its relationship to the x-and y-components of the momentum is pt2 = px2 + py2 and the net momentum of the particle is given by p2 = pt2 + pz2. |
Using Kaufmann and Bucherer's Data to Relate E, p & m

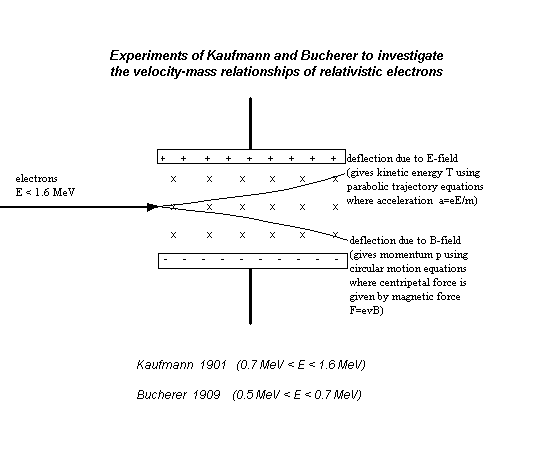
In 1901, W. Kaufmann did an experiment to investigate the relationship between velocity and mass for electrons in the 0.7MeV to 1.6 MeV energy range (W. Kaufmann, Gottingen Nach. 2, 143; 1901). Later, A. H. Bucherer did a similar experiment which included lower energy electrons (A. H. Bucherer, Ann. d. Phys. 28, 513; 1909).
In each case, deflection of electrons by a magnetic field yields momentum information while deflection by an electric field gives energy information. Thus, we can adapt the data of Kaufmann and Bucherer to show the relationship between E and p. We include simulated data for energies close to the electron rest energy to make your graph clearer.
To view and analyze the data, go to the data page.Questions:
- How can you use graphical analysis to discern a relationship between E and p using this data?
- What sort of function is a graph of E vs. p? of E2 vs. p2?
- What is E when p = 0? What does this indicate?
- What does the relationship between E and p look like when E is much greater than the rest energy?
- Can you infer a mathematical relationship between E, p, and m?
Last Update: August 30, 2012
Energy, Momentum, and Mass

Almost everyone is familar with Einstein's famous equation E=mc2. It indicates the energy content of a particle of mass m at rest. This is a special case. More generally, particle energy depends on particle motion as well as its mass. The energy of a particle (mass m moving with momentum p) is given by
E2 = (pc)2 + (mc2)2
or:
E2 = p2c2 + m2c4.
[eV]2 = [eV/c]2c2 + [eV/c2]2c4.
Take a look at what happens. All the c's cancel out:
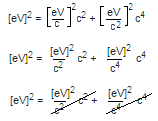 .
.
That is why particle physicists someitmes render this equation as
E2 = p2 + m2.
The c's are not exactly dropped; it is more like they are implied and it is understood that, given the proper units, they cancel.
Another thing: if the mass of a particle is very small and it has high momentum (p>>m, ignoring c's as we do above) - as in the case of many muons and electrons that come from decays of more massive particles in CMS - then the energy and the magnitude of the momentum are, in GeV units, almost the same (E≈p or E≈pc). Of course, for photons, which have no mass, E = p or E = pc is an exact equality and always true.Take a look at the screencast to see an example of how this can work out.
Learn more:
- construct the E-p-m relationship from data
- about those MeV and GeV units
- calculate the Z boson mass from CMS or ATLAS events