Energy, Momentum, and Mass

Almost everyone is familar with Einstein's famous equation E=mc2. It indicates the energy content of a particle of mass m at rest. This is a special case. More generally, particle energy depends on particle motion as well as its mass. The energy of a particle (mass m moving with momentum p) is given by

E2 = (pc)2 + (mc2)2

or:

E2 = p2c2 + m2c4.

You may have noticed that particle physicists often refer to particle masses and momenta in electron-volt energy units of MeV or GeV. They can do this because the speed of light, c, is a defined constant and can be used as a unit conversion factor. Then for energy in eV units, the corresponding momentum and mass units are eV/c and eV/c2, respectively. If you put these units in to the equation, you get:

[eV]2 = [eV/c]2c2 + [eV/c2]2c4.

Take a look at what happens. All the c's cancel out:

.

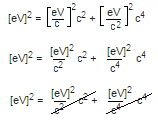That is why particle physicists sometimes render this equation as

E2 = p2 + m2. 

The c's are not exactly dropped; it is more like they are implied and it is understood that, given the proper units, they cancel.

Another thing: if the mass of a particle is very small and it has high momentum (p>>m, ignoring c's as we do above) - as in the case of many muons and electrons that come from decays of more massive particles in CMS - then the energy and the magnitude of the momentum are, in GeV units, almost the same (E≈p or E≈pc). Of course, for photons, which have no mass, E = p or E = pc is an exact equality and always true. Take a look at the screencast to see an example of how this can work out.

 

Learn more: