The MINERvA Masterclass Measurement

 

 

How do we go about the MINERvA masterclass measurement? Let's start with our goals:

  1. Separate signal from background in MINERvA
  2. Measure the neutrino beam energy in the Fermilab NuMI beamline
  3. Test models of interactions of neutrinos with nuclei.

Before step one, though, we need to get some background information on MINERvA and the physics of these interactions. Try these resources:

 

Job 1: Signal vs. Background

Here is what a signal event looks like in a side view of the MINERvA detector:

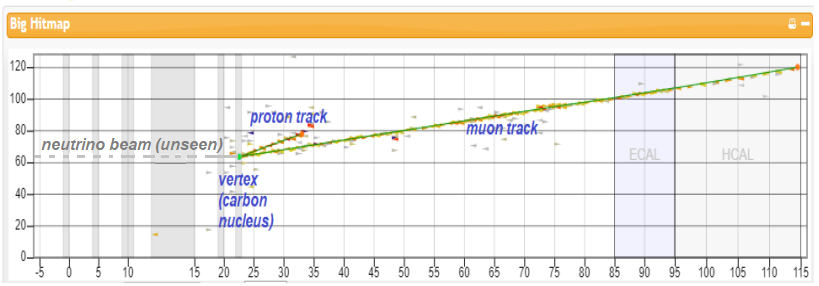
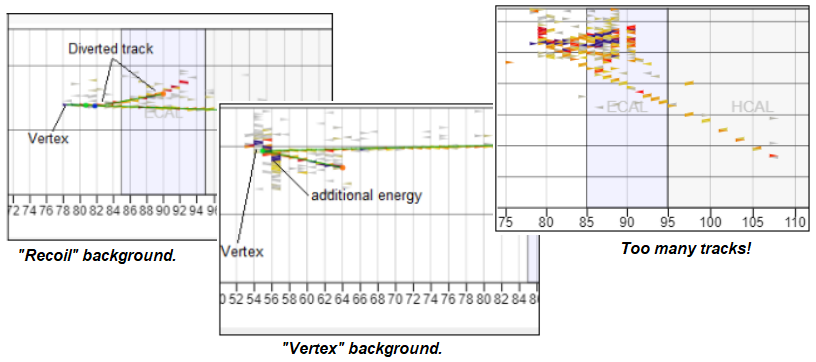
We cannot see (actually, the detector does not directly detect) the neutinos coming from the NuMI beam. We are looking for a particular interaction: a muon neutrino interacts with a neutron in the carbon nucleus, in the process transforming it into a muon and expelling the neutron transformed into a proton. MINERvA detects and measures these easily. The proton makes a short track and the muon makes a long track. The pattern in the image is a signal event. Anyting else is for us, background:

 

Job 2: Measure the NuMI Beam

Students. working in pairs, go through "Gates" which contain over 10 events each and choose one of them as signal - or none, if they cannot find any in that Gate. Each pair pair of students examines up to 50 Gates, looking for signal events. When they find them, they measure the momentum of each track using the tools in the ARACHNE Simple event display and transfer them to a spreadsheet.

Here is a short screencast describing the procedure:

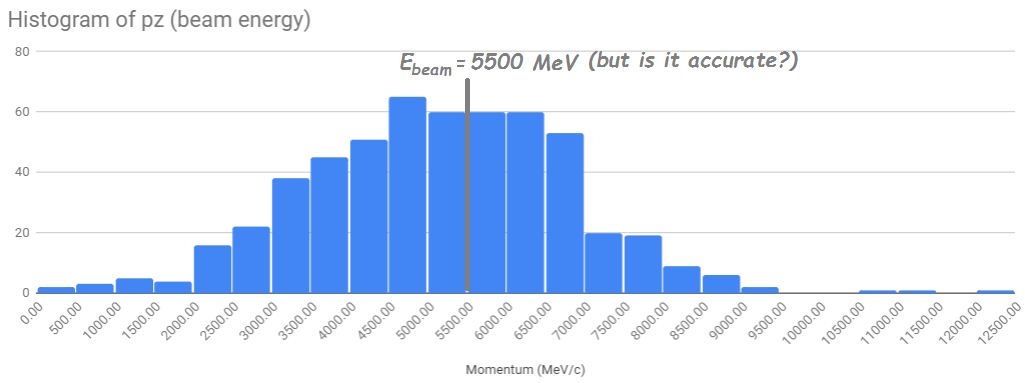
The entire class, contributing momentum measurements to the spreadsheet, builds up histograms of the net momentum in the x-, y-, and z-directions. The beam direction is defined as along the positive z-axis and the proton and neutron ought to have gotten their mometum in that direction from the neutrino, we can assume, approximately, that the central value of the momentum in z is the beam momentum. The number for the beam momentum in MeV/c is the same as the beam energy in GeV, so we have our measurement:

 

Job 3: Test Models of the Interaction

This is the most interesting but most subtle part of the measurement. Students check the histograms of momentum in the x- and y-directions. If the only momentum in the system is from the neutrino, there should be no momentum at all in these directions. Yet there is a distribution of momentum in each direction. With the guidance of the masterclass leader, students walk through the following logic:

  • If there is a distribution, something else must be adding momentum to the system. Does the "other" particle in the interaction have momentum? 
  • If there is a distribution in the momentum, that implies an overall uncertainty in the momentum. If we apply the Heisenberg Uncertainty Principle, that implies an uncertainty in the position of that "other particle" in the carbon nucleus. That uncertainty should correspond the the radius of the nucleus.
  • We can test this model by seeing if the uncertainty in position is similar to the publish radius of the carbon nucleus.
  • We can refine this model by treating the nucleus as a "Fermi gas" of particles.
  • Further refinements - a better model - can be tested by data from MINERvA.

 

To get going, get into the Masterclass Library (top right button)!

 

 

MINERvA Masterclass Pages